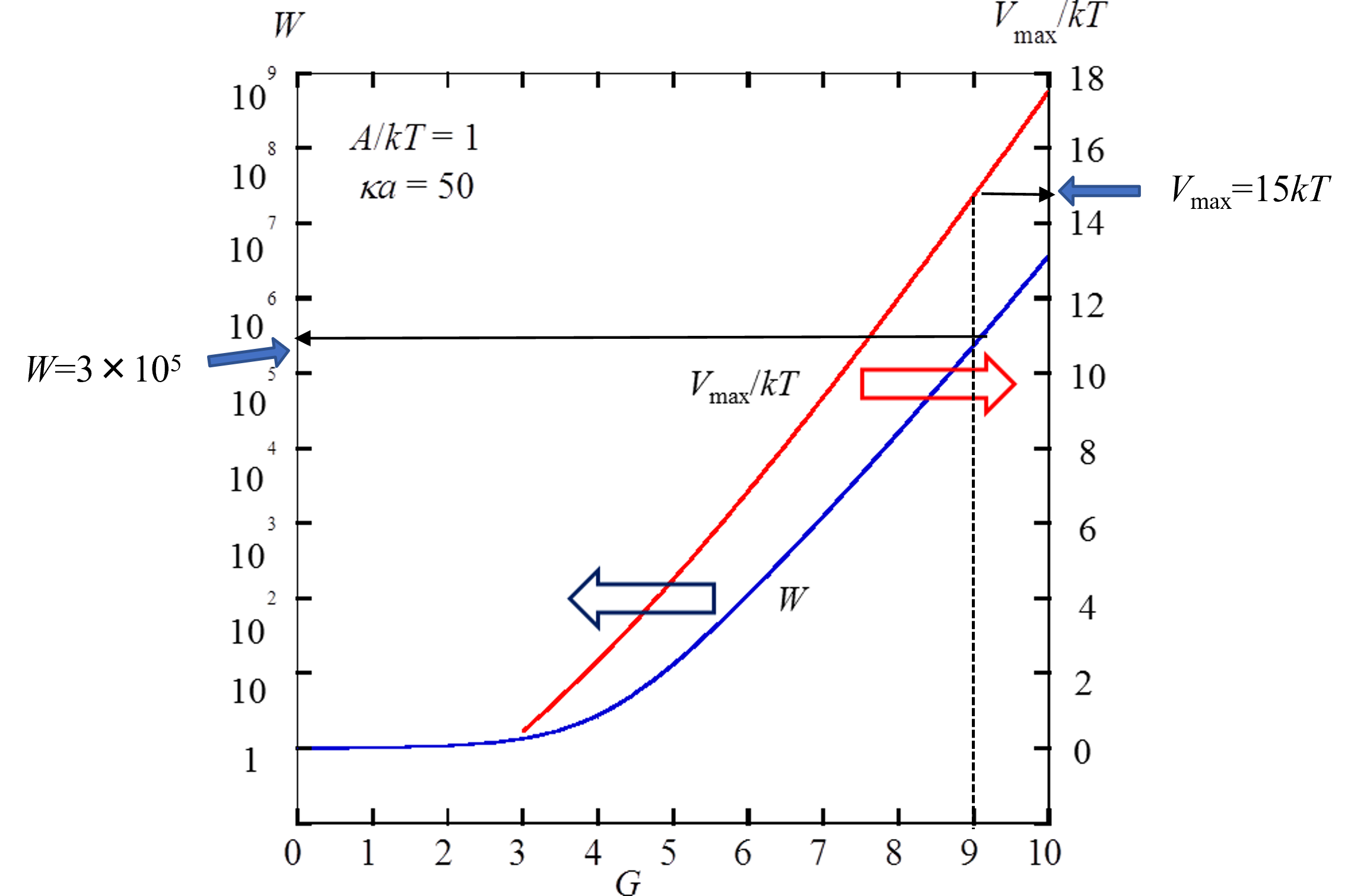
安定度比Wを用いて濃厚分散系の正確な分散安定性評価が可能に！

安定度比Wとは？

安定度比Wは粒子間の引力と反発力のバランスを示し、分散系の安定性を数学的に表現します。実験的に光散乱や沈降試験などの方法で測定され、分散の安定性を評価します。また、数理モデルに基づき、粒子間エネルギーの評価を通じてその値を計算によって求めることが出来ます。

濃厚分散系での安定性評価の際には、従来の評価方法では困難なケースが多くあります。

そこで、安定度比Wを用いることで、粒子間相互作用の詳細な制御が可能になり、コロイド粒子分散系の安定性が正確に評価できようになります。

粒子の凝集　-急速凝集と緩慢凝集-

粒子の凝集が起こる際の初期過程において、2個の1次粒子が不可逆的に結合(凝集)して2次粒子ができます。

凝集には、粒子間相互作用のポテンシャル障壁の有無で急速凝集と緩慢凝集に分けられます。

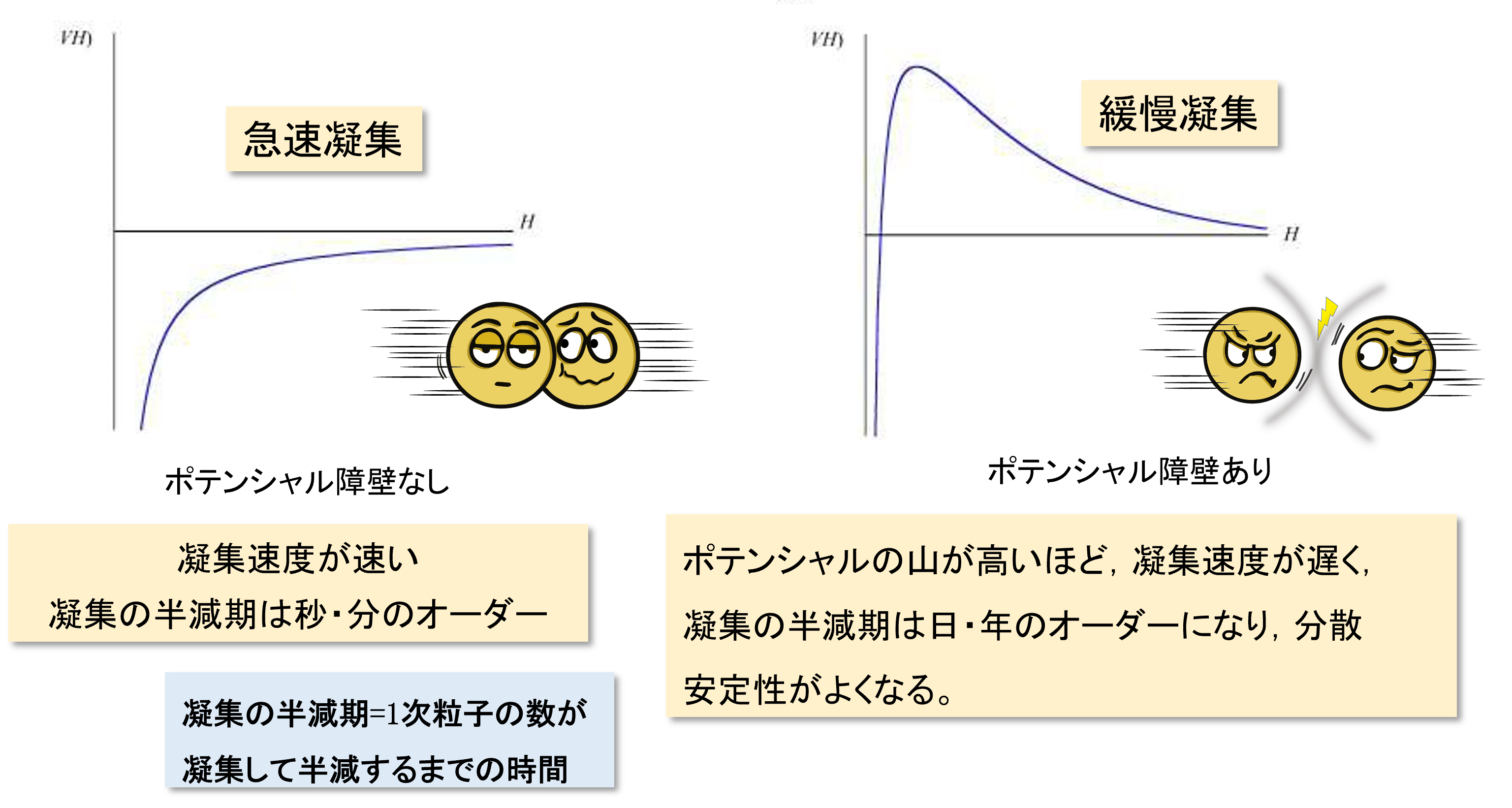
急速凝集：粒子間にvan der Waals引力相互作用のみ働く場合の凝集速度

緩慢凝集：van der Waals引力相互作用＋電気二重層静電相互作用が働く場合の凝集速度

凝集の半減期

スラリー中に含まれる一次粒子の数が、凝集によって半分になるまでの時間を、凝集の半減期といいます。

急速凝集の場合の半減期は、数秒～数分であるのに対し、緩慢凝集の場合は日・年といった単位であるため、スラリーの分散安定性は向上します。

安定度比Wは、凝集速度の遅くなる割合(半減期の長くなる度合い)を表します。

W＝緩慢凝集の半減期/急速凝集の半減期

安定度比Wが大きいほど、分散系は安定であるということができます。

上記のグラフは、粒子のポテンシャル山(Vmax)の代わりに安定度比Wを用いたグラフです。

安定性の基準として、ポテンシャルの山の高さVmaxが熱エネルギーkTの15倍以上の場合、安定度比Wは3×10^5以上となります。急速凝集の半減期が1分と仮定すると、上記の「W＝緩慢凝集の半減期/急速凝集の半減期」という計算式から、凝集の半減期は約208日になることが導かれます。

このように、安定度比Wを用いることで、粒子間に働く全相互作用のポテンシャル曲線における山の高さVmaxよりもコロイド粒子分散系の安定性が正確に評価できようになります。

関連製品・サービス