【第四回】「分散安定性」の制御について－粒子間に働く斥力と粒子間距離

前回は「分散性」と「凝集力」について紹介した。

今回は、「分散安定性」の制御について考えてみよう。

 

「分散安定性」の鍵を握るのは、DLVO理論の中の静電的斥力や粒子表面に吸着した高分子である。前者の静電的斥力は、粒子同士が近づき粒子間距離が短くなると（拡散）電気二重層が重なり、重畳部分は溶液バルク相のイオン濃度よりも対（たい）イオン濃度が高くなり過剰浸透圧が働く。この過剰浸透圧が静電的斥力の源となる。

 

一方、後者の高分子吸着による分散安定化機構は、二つあって、

① 吸着高分子の鎖同士が重なり合うと、重なり合っていない部分に比べて高分子鎖濃度が高くなるので、浸透圧によって周りから溶媒が流入して粒子間に斥力が働く、という浸透圧効果と、

② 鎖が接近することにより一つの鎖の自由体積内には他の鎖が入れず、広がった鎖が圧縮されてしまい、鎖が元の状態に戻ろうとして粒子間に斥力が働く、という立体障害効果がある。

 

いずれにしても粒子間距離に依存してこれら斥力が作用する領域が決まるので、ここでは粒子間距離の計算の仕方について少し触れておくことにする。

ここで断わっておくが、前回の凝集力と大きく異なるのは、凝集力（London-van der Waals力）が概ね10nm以下の距離で働くのに対し、斥力は10nm以上の比較的遠い距離で働く点である。

 

まず、前回のコラムで粒子間相互作用のポテンシャル曲線を示したが、粒子間距離に依存して変化していたことを思い出して頂きたい。横軸の粒子間距離は実は粒子の濃度だけではなく、粒子の大きさにも依存して決まる。この点が重要である。

つまり、粒子濃度が同じ20vol％であっても500nmの粒子の場合と20nmの粒子の場合では大きく異なる。

東京農工大の神谷先生らのグループがWoodcockの式を用いて計算した例があるので下図に示す。

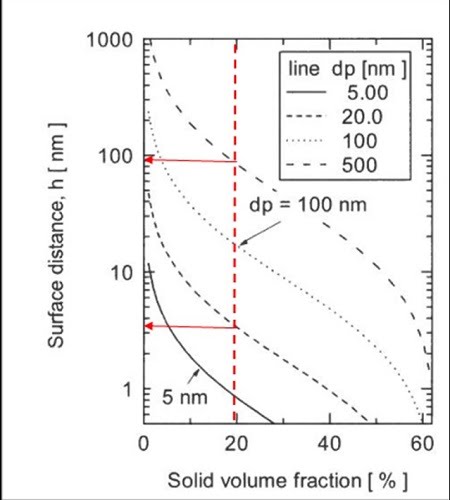
この図からも明らかなように、500nmの粒子の場合には粒子の表面間距離は約100nmであるのに対し、20nmの粒子の場合には約4nmとなっている。

したがって、濃厚分散液を扱う場合には、粒子径と濃度から粒子間距離を計算し、おおよその状況を想像しながら分散安定性の制御因子を考察する必要がある。

例えば、静電的斥力で分散安定性を制御しようとするとき、電気二重層の厚さは、z-z型電解質溶液の場合、z=1（KCl,NaCl,KNO3など）で

となるので、20nmの粒子の場合、20vol％では粒子表面間距離が約4nmなので、0.1mol/Lの電解質濃度であれば二重層は重ならないが、0.001mol/Lになると二重層がはじめから重なってしまう計算になるので、実際にこの濃度で調製すると凝集粒子ができることになる。

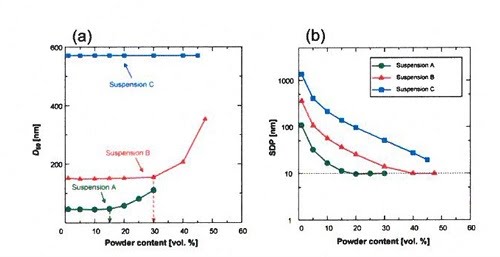
粒子径が570nmから43nmまでの3種の粒子径の系で濃厚アルミナスラリーを調製して超音波法で粒子径分布を求めた東工大・磯部先生と産総研・堀田先生らのグループの結果を示すが、いずれも粒子間距離が10nm程度に近づく濃度になると、全ての粒子がもはや１次粒子として存在できなくなり、凝集粒子が含まれてくることが実験結果からも確認されている。

この系では、電解質の代わりにポリアクリル酸アンモニウムの高分子が分散剤として用いられているので、電解質濃度から計算される二重層厚さをそのままあてはめて解釈することはできないが、

少なくとも粒子間距離が短くなってくると、電気二重層だけでなく、高分子吸着層同士の相互作用が作用する距離になり、ある程度凝集粒子が残り、粒子間の距離が短いために分散安定性を制御するのが難しくなってくることが分かる。

 

今回は粒子間距離や電気二重層の厚さの詳細な計算方法等を省いたが、このコラムでは順次それら計算法等も紹介してゆこうと思う。